---

Manual Reference Pages  - cos (3fortran)

---

NAME

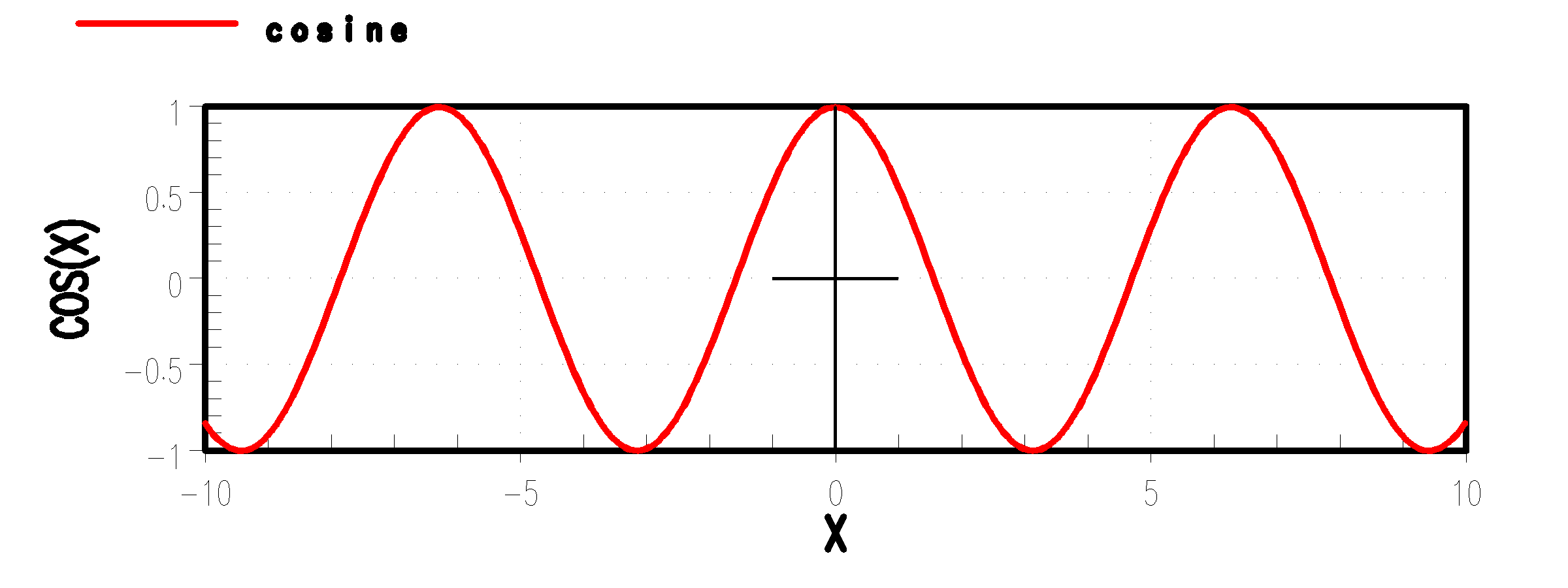
COS(3) - [MATHEMATICS:TRIGONOMETRIC] Cosine function

SYNOPSIS

result = cos(x)

         elemental TYPE(kind=KIND) function cos(x)

          TYPE(kind=KIND),intent(in) :: x

CHARACTERISTICS

o	X is of type real or complex of any valid kind.
o	The returned value will be of the same type and kind as the argument X.

DESCRIPTION

COS(3) computes the cosine of an angle X given the size of the angle in radians.

The cosine of a real value is the ratio of the adjacent side to the hypotenuse of a right-angled triangle.

OPTIONS

o	X : The angle in radians when X is of type real. If X is of type complex, its real part is regarded as a value in radians, often called the phase.

RESULT

The return value is the cosine of X.

If X is type real, the return value lies in the range -1 <= COS(X) <= 1 [char46]

EXAMPLES

Sample program:

    program demo_cos
    implicit none
    real,parameter       :: PI=atan(1.0d0)*4.0d0
    real                 :: val
    character,parameter  :: nl=NEW_LINE(’A’)
       write(*,’(*(g0))’,advance=’no’) &

    ’basics:’,                                             nl, &
    ’ COS(0.0) =         ’, cos(0.0),                      nl, &
    ’ COS(PI) =          ’, cos(PI),                       nl, &
    ’ ’,                                                   nl, &
    ’X may be any real value’,                             nl, &
    ’ COS(222*PI) =      ’, cos(222*PI),                   nl, &
    ’ COS(-333*PI) =     ’, cos(-333*PI),                  nl, &
    ’ ’,                                                   nl, &
    ’note: probably not exactly zero ....’,                nl, &
    ’ COS(PI/2.0)=       ’, cos(PI/2.0),                   nl, &
    ’ EPSILON=           ’, epsilon(PI),                   nl, &
    ’ ’,                                                   nl, &
    ’COS() is elemental’,                                  nl, &
    ’ COS([0.0,PI/4,PI/2,PI*3/4,PI]) = ’,                  nl
       write(*,’(*(1x,g0,1x))’) COS([0.0,PI/4,PI/2,PI*3/4,PI])

       write(*,’(*(g0))’,advance=’no’) &
    ’ ’,                                                   nl, &
    ’Law of Cosines:’,                                     nl, &
    ’ ’,                                                   nl, &
    ’right triangle’,                                      nl, &
    two_sides_and_degrees_between(3.0,4.0,90.0),           nl, &
    ’equilateral’,                                         nl, &
    two_sides_and_degrees_between(3.3,3.3,60.0),           nl, &
    ’ ’,                                                   nl, &
    ’Dusty Corners:’,                                      nl, &
    ’ ’,                                                   nl, &
    ’If very large, representable numbers are far apart’,  nl, &
    ’so adding or subtracting a few radians can not even’, nl, &
    ’change the value! Note the expected values here:’,    nl
       val=0.0
       call delta( val-2.0, val-1.0 )

       write(*,’(a)’) ’but look at the same call when the values are huge;’
       val=huge(0.0)/1000
       call delta( val-2.0, val-1.0 )

    contains

    subroutine delta(A,B)
    real(kind=kind(0.0)),intent(in) :: a,b
    print ’(a,t30,g0)’ , &
    ’ A=                     ’, A, &
    ’ B=                     ’, B, &
    ’ B-A=                   ’, B-A, &
    ’ COS(A*PI)=             ’, cos(A*PI), &
    ’ COS(B*PI)=             ’, cos(B*PI), &
    ’ spacing(A)=            ’, spacing(A), &
    ’ COS((B-A)*PI)=         ’, cos((B-A)*PI), &
    ’ COS(B*PI)-COS(A*PI)=   ’, cos(B*PI)-cos(A*PI), &
    repeat(’=’,40)
    end subroutine delta

    function two_sides_and_degrees_between(a,b,X) result(str)
    real,intent(in)              :: a,b,X
    real                         :: c
    real,parameter               :: PI = atan(1.0d0) * 4.0d0
    real,parameter               :: degrees_to_radians = PI / 180.0
    character,parameter          :: nl=NEW_LINE(’A’)
    character(len=:),allocatable :: str
    ! The law of cosines states that for a
    ! triangle with sides of length a, b, and c
    ! that if the angle X is formed by sides a and
    ! b that the length of the third side c is
    !
       c = sqrt( a**2 + b**2 - 2*a*b*cos(degrees_to_radians*X) )
       allocate( character(len=132) :: str )
       write(str,’(*(g0))’)&
       ’For sides A=’,a,’, B=’,b,’ and X=’,x,’ degrees,’,nl,’side C=’,c
       str=trim(str)
    !
    !                        \
    !                       / \
    !                      / Y \
    !                     /     \
    !                    /       \
    !                   /         \
    !                b /           \ c
    !                 /             \
    !                /               \
    !               /                 \
    !              /                   \
    !             / X                 Z \
    !            -------------------------
    !                        a
    end function two_sides_and_degrees_between
    end program demo_cos

Results:

     > basics:
     >  COS(0.0) =         1.00000000
     >  COS(PI) =          -1.00000000
     >
     > X may be any real value
     >  COS(222*PI) =      1.00000000
     >  COS(-333*PI) =     -1.00000000
     >
     > note: probably not exactly zero ....
     >  COS(PI/2.0)=       -0.437113883E-7
     >  EPSILON=           0.119209290E-6
     >
     > COS() is elemental
     >  COS([0.0,PI/4,PI/2,PI*3/4,PI]) =
     >  1.00000000  0.707106769  -0.437113883E-7  -0.707106769  -1.00000000
     >
     > Law of Cosines:
     >
     > right triangle
     > For sides A=3.00000000, B=4.00000000 and X=90.0000000 degrees,
     > side C=5.00000000
     > equilateral
     > For sides A=3.29999995, B=3.29999995 and X=60.0000000 degrees,
     > side C=3.29999995
     >
     > Dusty Corners:
     >
     > If very large, representable numbers are far apart
     > so adding or subtracting a few radians can not even
     > change the value! Note the expected values here:
     >  A=                          -2.00000000
     >  B=                          -1.00000000
     >  B-A=                        1.00000000
     >  COS(A*PI)=                  1.00000000
     >  COS(B*PI)=                  -1.00000000
     >  spacing(A)=                 0.238418579E-6
     >  COS((B-A)*PI)=              -1.00000000
     >  COS(B*PI)-COS(A*PI)=        -2.00000000
     > ========================================
     > but look at the same call when the values are huge;
     >  A=                          0.340282343E+36
     >  B=                          0.340282343E+36
     >  B-A=                        0.00000000
     >  COS(A*PI)=                  0.766595423
     >  COS(B*PI)=                  0.766595423
     >  spacing(A)=                 0.396140813E+29
     >  COS((B-A)*PI)=              1.00000000
     >  COS(B*PI)-COS(A*PI)=        0.00000000
     > ========================================

STANDARD

FORTRAN 77

SEE ALSO

ACOS(3), SIN(3), TAN(3)

RESOURCES

o	Wikipedia:sine and cosine

Fortran intrinsic descriptions

---